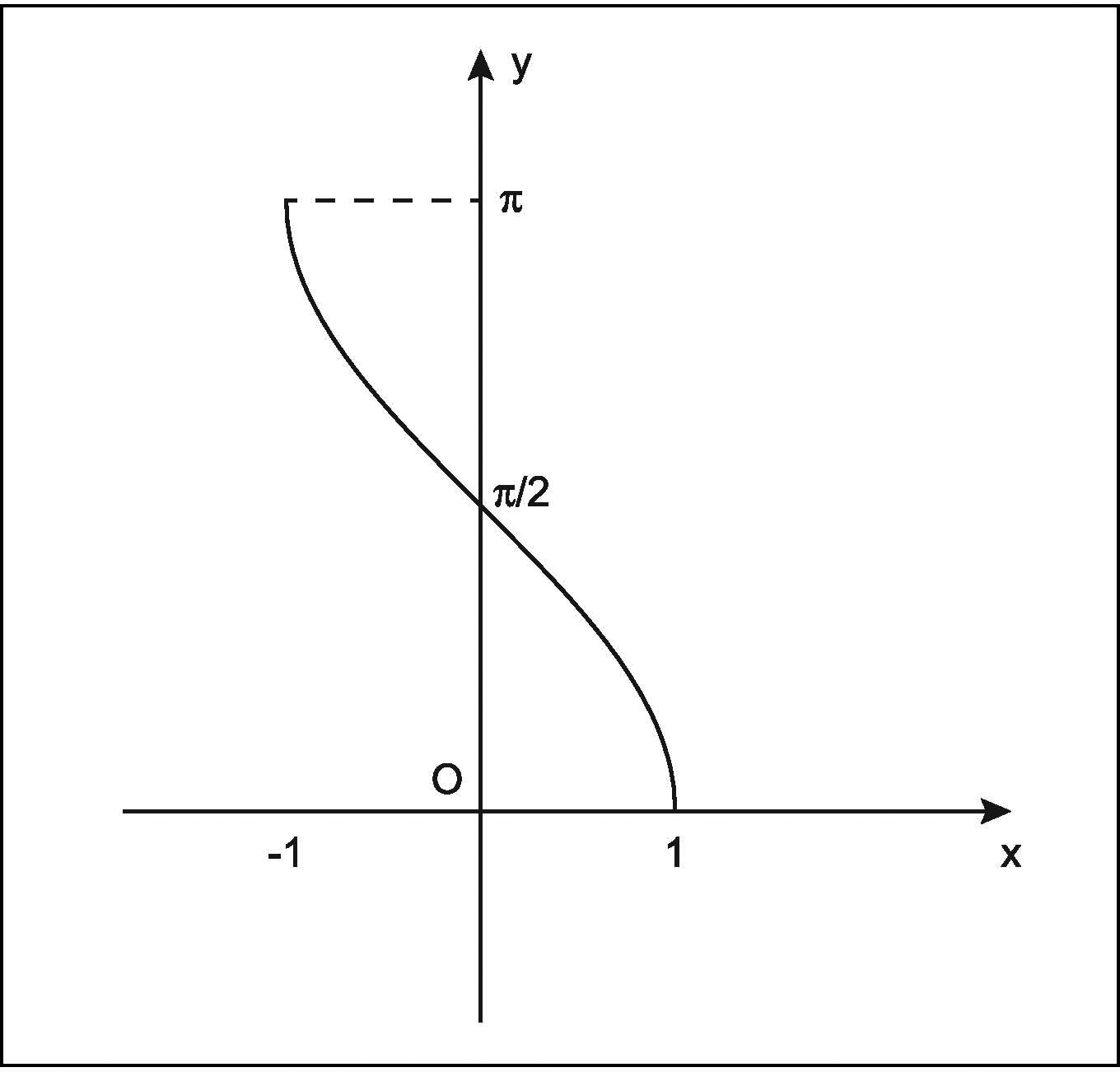
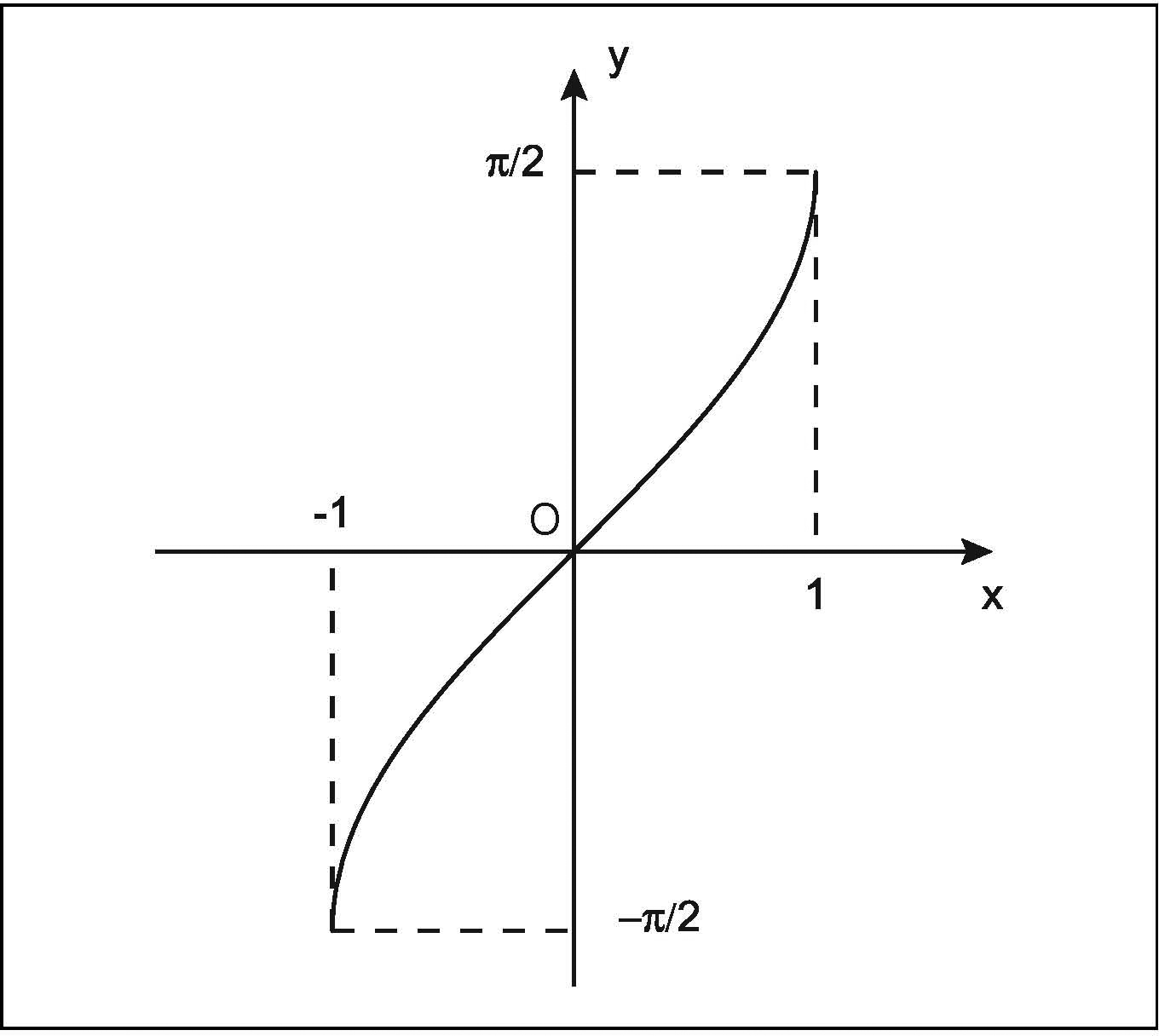Arcotangente — arctan(x) ✔
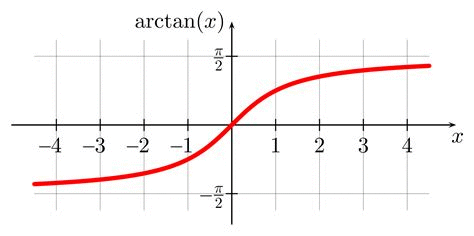
Dominio: ℝ
Codominio: (−π/2, π/2)
Parità: Dispari (simmetria rispetto all'origine)
Inversa: tan(x)
Continuità: ✔ continua su ℝ
Derivabilità: ✔ derivabile su ℝ
Monotonia: Strettamente crescente ➕
Concavità: Convessa su x < 0, concava su x > 0
Asintoti: Orizzontali: y = ±π/2
Limiti notevoli: lim(x→±∞) arctan(x) = ±π/2
Derivata: 1 / (1 + x2)
Integrale: x•arctan(x) − ½•ln(1 + x2) + C
Taylor: ∑n=0∞ [(−1)n • x2n+1] / (2n + 1)
Sviluppo di Taylor: arctan(x) ≈ x − x3/3 + x5/5 − x⁷/7 + …
Stima asintotica: arctan(x) ≈ x − x3/3 + o(x3) per |x| ≪ 1
Derivata della serie: ∑n=0∞ (−1)n x2n
Integrale della serie: ∑n=0∞ [(−1)n • x2n+2] / ( (2n + 1)(2n + 2) )
Identità: arctan(x) + arctan(1/x) = π/2 (x > 0)
Applicazioni: trigonometria inversa, modelli di saturazione
Esempi: arctan(1) = π/4, arctan(−1) = −π/4, arctan(10) ≈ 1.47